leetcode数据结构刷题(一)

Leetcode 数据结构练习

# 数组

# 最大子序和

思路：动态规划

class Solution {
    public int maxSubArray(int[] nums) {
        int pre = 0,maxn = nums[0];     
        for (int x:nums){
            pre = Math.max(pre+x,x);
            maxn = Math.max(pre,maxn);
        }
        return maxn;
    }
}

# 两数之和

哈希表降时间复杂度从 o (n) 到 o (1)

创建一个哈希表，对于每一个 x ，我们首先查询哈希表中是否存在 target - x ，然后将 x 插入到哈希表中，即可保证不会让 x 和自己匹配。

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> hashtable = new HashMap<Integer, Integer>();
        for (int i = 0; i < nums.length; ++i) {
            if (hashtable.containsKey(target - nums[i])) {
                return new int[]{hashtable.get(target - nums[i]), i};
            }
            hashtable.put(nums[i], i);
        }
        return new int[0];
    }
}

# 合并两个有序数组

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。
示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

exp

一、双指针

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int p1 = 0, p2 = 0;
        int sorted[m + n];
        int cur;
        while (p1 < m || p2 < n) {
            if (p1 == m) {
                cur = nums2[p2++];
            } else if (p2 == n) {
                cur = nums1[p1++];
            } else if (nums1[p1] < nums2[p2]) {
                cur = nums1[p1++];
            } else {
                cur = nums2[p2++];
            }
            sorted[p1 + p2 - 1] = cur;
        }
        for (int i = 0; i != m + n; ++i) {
            nums1[i] = sorted[i];
        }
    }
};

复杂度分析

时间复杂度：O (m+n)
指针移动单调递增，最多移动 m+n 次，因此时间复杂度为 O (m+n)。

空间复杂度：O (m+n)。
需要建立长度为 m+n 的中间数组 sorted。

二、逆向双指针

从后向前遍历，将两者较大的元素放在 nums 数组的后面而不会被覆盖，降低了空间复杂度为 O (1)

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int p1 = m - 1, p2 = n - 1;
        int tail = m + n - 1;
        int cur;
        while (p1 >= 0 || p2 >= 0) {
            if (p1 == -1) {
                cur = nums2[p2--];
            } else if (p2 == -1) {
                cur = nums1[p1--];
            } else if (nums1[p1] > nums2[p2]) {
                cur = nums1[p1--];
            } else {
                cur = nums2[p2--];
            }
            nums1[tail--] = cur;
        }
    }
};

# 两个数组的交集

一、哈希表

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        if (nums1.size() > nums2.size()) {
            return intersect(nums2, nums1);
        }
        unordered_map <int, int> m;
        for (int num : nums1) {
            ++m[num];
        }
        vector<int> intersection;
        for (int num : nums2) {
            if (m.count(num)) {
                intersection.push_back(num);
                --m[num];
                if (m[num] == 0) {
                    m.erase(num);
                }
            }
        }
        return intersection;
    }
};

时间复杂度：O (m+n), 空间复杂度：O (min (m,n))

二、双指针排序

```

### 买卖股票的最佳时机

>输入：[7,1,5,3,6,4]
>输出：5
>解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
>     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

exp:

**动态规划**

(来自题解）考虑每次如何获取最大收益，第i天的最大收益通过前i天的最低点就可以算出来。而第i天以前（包括第i天）的最低点和i-1天的最低点有关，因此动态方程为

dp[i] = min(d[i-1],prices[i])
其中dp[0]=prices[0],然后动态计算之后的就可以了。 得到了前i天的最低点以后，只需要维护一个max用来保存最大收益就可以了。 时间复杂度为O(n),一次遍历，空间复杂度O（n）的动态规划，代码如下：

```java
        //dp[i]表示截止到i，价格的最低点是多少   dp[i]=min(dp[i-1],nums[i])
        int max = 0;
        int[] dp = new int[prices.length];
        dp[0] = prices[0];
        for (int i = 1; i < prices.length; i++) {
            dp[i] = (dp[i - 1] < prices[i]) ? dp[i - 1] : prices[i];
            max = (prices[i] - dp[i]) > max ? prices[i] - dp[i] : max;
        }
        return max;

接着考虑优化空间，仔细观察动态规划的辅助数组，其实每一次只用到了 dp [-1] 这一个空间，因此可以把数组改成单个变量 dp 来存储截止到第 i 天的价格最低点。优化之后的代码就是题解中的方法二。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int inf = 1e9;
        int minprice = inf, maxprofit = 0;
        for (int price: prices) {
            maxprofit = max(maxprofit, price - minprice);
            minprice = min(price, minprice);
        }
        return maxprofit;
    }
};

时间复杂度 O (n), 空间复杂度 O (1)

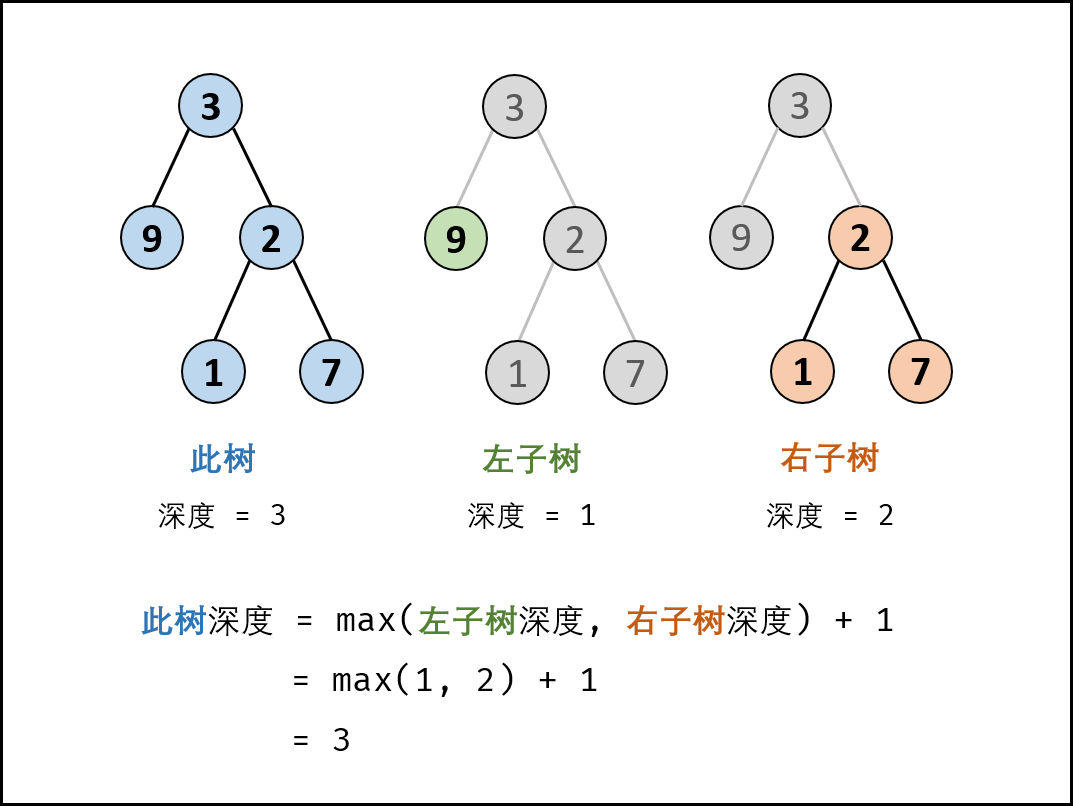
# 树和二叉树

# 二叉树的深度

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

​ 3

/
9 20
/
15 7
返回它的最大深度 3 。

# 法一：DFS

树的深度等于左子树的深度和右子树深度的最大值 + 1

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==nullptr)
            return 0;
        int leftdeep=maxDepth(root->left);
        int rightdeep = maxDepth(root->right);
        return max(leftdeep,rightdeep)+1;
    }
};

# 对称二叉树

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1
/
2 2
/ \ /
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

1
/
2 2
\
3 3

题解：

双指针递归剪枝，结束条件为左右指针同时都为空指针返回 true，如果值不同或只有一个为空返回 false

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(root==NULL)
            return true;
        TreeNode *l=root;
        TreeNode *r=root;
        return recv(l,r);
    }
    bool recv(TreeNode * l,TreeNode *r){
        if(l==NULL&&r==NULL)
            return true;
        if(l==NULL||r==NULL||l->val!=r->val)
            return false;     //上面两个位置不能调换
    
        return recv(l->left,r->right)&&recv(l->right,r->left);
    
    }
};

# 平衡二叉树

平衡二叉树的定义是：二叉树的每个节点的左右子树的高度差的绝对值不超过 11，则二叉树是平衡二叉树。根据定义，一棵二叉树是平衡二叉树，当且仅当其所有子树也都是平衡二叉树，因此可以使用递归的方式判断二叉树是不是平衡二叉树，递归的顺序可以是自顶向下或者自底向上。

# 法一： 自顶向下递归

class Solution {
public:
    int height(TreeNode* root) {
        if (root == NULL) {
            return 0;
        } else {
            return max(height(root->left), height(root->right)) + 1;
        }
    }

    bool isBalanced(TreeNode* root) {
        if (root == NULL) {
            return true;
        } else {
            return abs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
        }
    }
};

复杂度分析

时间复杂度：O (n^2)，其中 n 是二叉树中的节点个数。
最坏情况下，二叉树是满二叉树，需要遍历二叉树中的所有节点，时间复杂度是 O (n)。
对于节点 p，如果它的高度是 d，则 \texttt {height}§height§ 最多会被调用 dd 次（即遍历到它的每一个祖先节点时）。对于平均的情况，一棵树的高度 h 满足 O (h)=O (\log n) O (h)=O (logn)，因为 d \leq hd≤h，所以总时间复杂度为 O (n \log n)。对于最坏的情况，二叉树形成链式结构，高度为 O (n)，此时总时间复杂度为 O (n^2)

空间复杂度：O (n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n。

# 法二： 自底向上递归

class Solution {
public:
    int height(TreeNode* root) {
        if (root == NULL) {
            return 0;
        }
        int leftHeight = height(root->left);
        int rightHeight = height(root->right);
        if (leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1) {
            return -1;
        } else {
            return max(leftHeight, rightHeight) + 1;
        }
    }

    bool isBalanced(TreeNode* root) {
        return height(root) >= 0;
    }
};

复杂度分析

时间复杂度：O (n)，其中 n 是二叉树中的节点个数。使用自底向上的递归，每个节点的计算高度和判断是否平衡都只需要处理一次，最坏情况下需要遍历二叉树中的所有节点，因此时间复杂度是 O (n)。

空间复杂度：O (n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n。

# 二叉树剪枝

后序遍历 dfs

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {
        if(root == NULL)
            return NULL;
        TreeNode *leftnode = pruneTree(root->left);
        TreeNode *rightnode = pruneTree(root->right);
        if(root->val==0 && leftnode==NULL&&rightnode == NULL )
            return nullptr;
        root->left = leftnode;
        root->right= rightnode;
        return root;
    }   
};

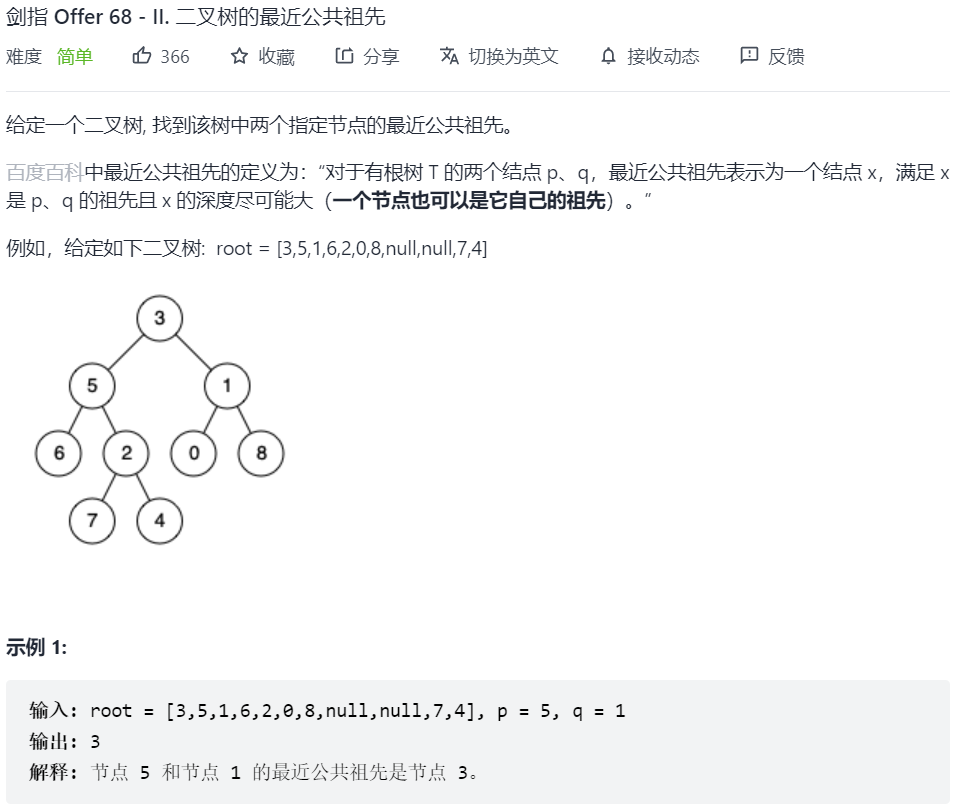
# 寻找最近公共祖先

# 法一：递归

class Solution {
public:
    TreeNode* ans;
    bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr) return false;   
        bool lson = dfs(root->left, p, q);
        bool rson = dfs(root->right, p, q);
        if ((lson && rson) || ((root->val == p->val || root->val == q->val) && (lson || rson)))//lson&&rson表示左右子树均包含p或q节点，root恰好是p或q且它的左子树或右子树有一个包含了另一个节点的情况
        {
            ans = root;
        } 
        return lson || rson || (root->val == p->val || root->val == q->val);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        dfs(root, p, q);
        return ans;
    }
};

# 法二：存储父节点

从根节点开始遍历整棵二叉树，用哈希表记录每个节点的父节点指针。
从 p 节点开始不断往它的祖先移动，并用数据结构记录已经访问过的祖先节点。
同样，我们再从 q 节点开始不断往它的祖先移动，如果有祖先已经被访问过，即意味着这是 p 和 q 的深度最深的公共祖先，即 LCA 节点。

class Solution {
public:
    unordered_map<int, TreeNode*> fa;
    unordered_map<int, bool> vis;
    void dfs(TreeNode* root){
        if (root->left != nullptr) {
            fa[root->left->val] = root;
            dfs(root->left);
        }
        if (root->right != nullptr) {
            fa[root->right->val] = root;
            dfs(root->right);
        }
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        fa[root->val] = nullptr;
        dfs(root);
        while (p != nullptr) {
            vis[p->val] = true;
            p = fa[p->val];
        }
        while (q != nullptr) {
            if (vis[q->val]) return q;
            q = fa[q->val];
        }
        return nullptr;
    }
};

# 二叉搜索树

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

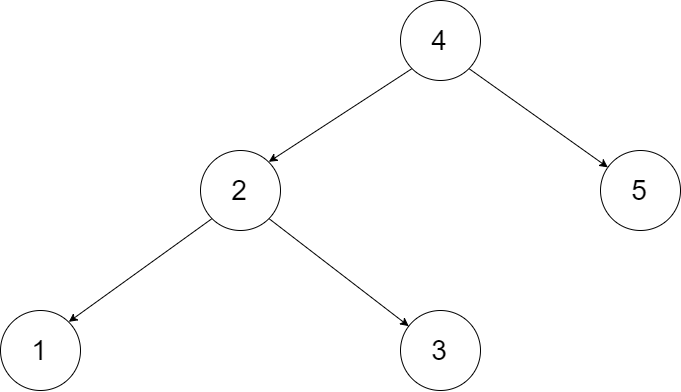
为了让您更好地理解问题，以下面的二叉搜索树为例：

我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

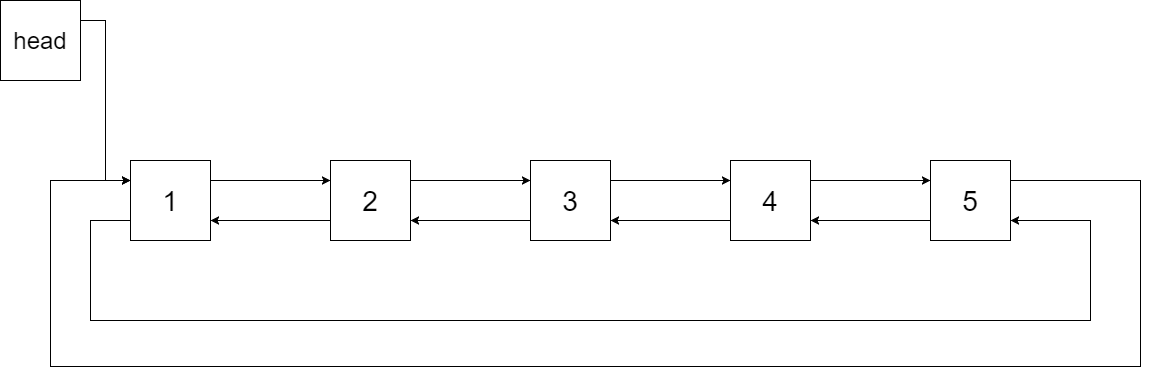
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

• 思路：

二叉搜索树 转换成一个 “排序的循环双向链表” ，其中包含三个要素：

排序链表： 节点应从小到大排序，因此应使用 中序遍历 “从小到大” 访问树的节点。
双向链表： 在构建相邻节点的引用关系时，设前驱节点 pre 和当前节点 cur ，不仅应构建 pre.right = cur ，也应构建 cur.left = pre 。
循环链表： 设链表头节点 head 和尾节点 tail ，则应构建 head.left = tail 和 tail.right = head 。

• 算法流程

dfs (cur): 递归法中序遍历；

终止条件： 当节点 cur 为空，代表越过叶节点，直接返回；
递归左子树，即 dfs (cur.left) ；
构建链表：
当 pre 为空时： 代表正在访问链表头节点，记为 head ；
当 pre 不为空时： 修改双向节点引用，即 pre.right = cur ， cur.left = pre ；
保存 cur ： 更新 pre = cur ，即节点 cur 是后继节点的 pre ；
递归右子树，即 dfs (cur.right) ；
treeToDoublyList(root)：

特例处理： 若节点 root 为空，则直接返回；
初始化： 空节点 pre ；
转化为双向链表： 调用 dfs (root) ；
构建循环链表： 中序遍历完成后，head 指向头节点， pre 指向尾节点，因此修改 head 和 pre 的双向节点引用即可；
返回值： 返回链表的头节点 head 即可；

class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        if(root == nullptr) return nullptr;
        dfs(root);
        head->left = pre;
        pre->right = head;
        return head;
    }
private:
    Node *pre, *head;
    void dfs(Node* cur) {
        if(cur == nullptr) return;
        dfs(cur->left);
        if(pre != nullptr) pre->right = cur; //用pre来查找
        else head = cur; //找到头结点
        cur->left = pre;
        pre = cur;
        dfs(cur->right);
    }
};

复杂度分析：
时间复杂度 O (N)： N 为二叉树的节点数，中序遍历需要访问所有节点。
空间复杂度 O (N) ： 最差情况下，即树退化为链表时，递归深度达到 N，系统使用 O (N) 栈空间。