2022-01-30 e5f15bd8e1aec34627e169c0baec9b42 99+ 7 m 1.1 k0 visits

leetcode数据结构刷题（二）

二叉搜索树相关

# 0x01 二叉树最底层最左边的值

给定一个二叉树的 根节点 root ，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

1 2	输入: [1,2,3,4,null,5,6,null,null,7] 输出: 7

# 法一：前序遍历 DFS

使用 DFS 递归遍历树的所有节点，记录当前节点的层级 level 与已遍历节点的最大层级 maxLevel
每当 level 超过 maxLevel 时，将当前节点赋值给 res，另外更新 maxLevel
遍历完成后，res 就是要找的节点，返回该节点的值即可

遍历到新的一层的第一个节点为最底层，最左边的节点

class Solution {
public:
    int res = 0;
    int maxlevel=-1;
    int findBottomLeftValue(TreeNode* root) {
     	dfs(root,0);
        return res;
    }
    void dfs(TreeNode * root,int level){
		if(root==NULL)
            return ;
        if(level>maxlevel){
            res = root->val;
            maxlevel = level;
        }
        dfs(root->left,level+1);
        dfs(root->right,level+1);
    }   
};

# 法二：层序遍历 BFS

更新每层第一个元素值，取最后一次更新值

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
      queue<TreeNode*> q;
      q.push(root);
      int leftnode;
      while(!q.empty()){
          int size = q.size();
          for (int i=size;i;i--){
              auto node = q.front();
              if(i==size)
                  leftnode = node->val;
              q.pop();
              if(node->left) q.push(node->left);
              if(node->right) q.push(node->right);
          }
      }
        return leftnode;
    }
};

# 0x02 往完全二叉树添加节点

完全二叉树是每一层（除最后一层外）都是完全填充（即，节点数达到最大，第 n 层有 2n-1 个节点）的，并且所有的节点都尽可能地集中在左侧。

设计一个用完全二叉树初始化的数据结构 CBTInserter，它支持以下几种操作：

CBTInserter (TreeNode root) 使用根节点为 root 的给定树初始化该数据结构；
CBTInserter.insert (int v) 向树中插入一个新节点，节点类型为 TreeNode，值为 v 。使树保持完全二叉树的状态，并返回插入的新节点的父节点的值；
CBTInserter.get_root () 将返回树的根节点。

示例 1：

输入：inputs = ["CBTInserter","insert","get_root"], inputs = [[[1]],[2],[]]
输出：[null,1,[1,2]]

输入：inputs = ["CBTInserter","insert","insert","get_root"], inputs = [[[1,2,3,4,5,6]],[7],[8],[]]
输出：[null,3,4,[1,2,3,4,5,6,7,8]]

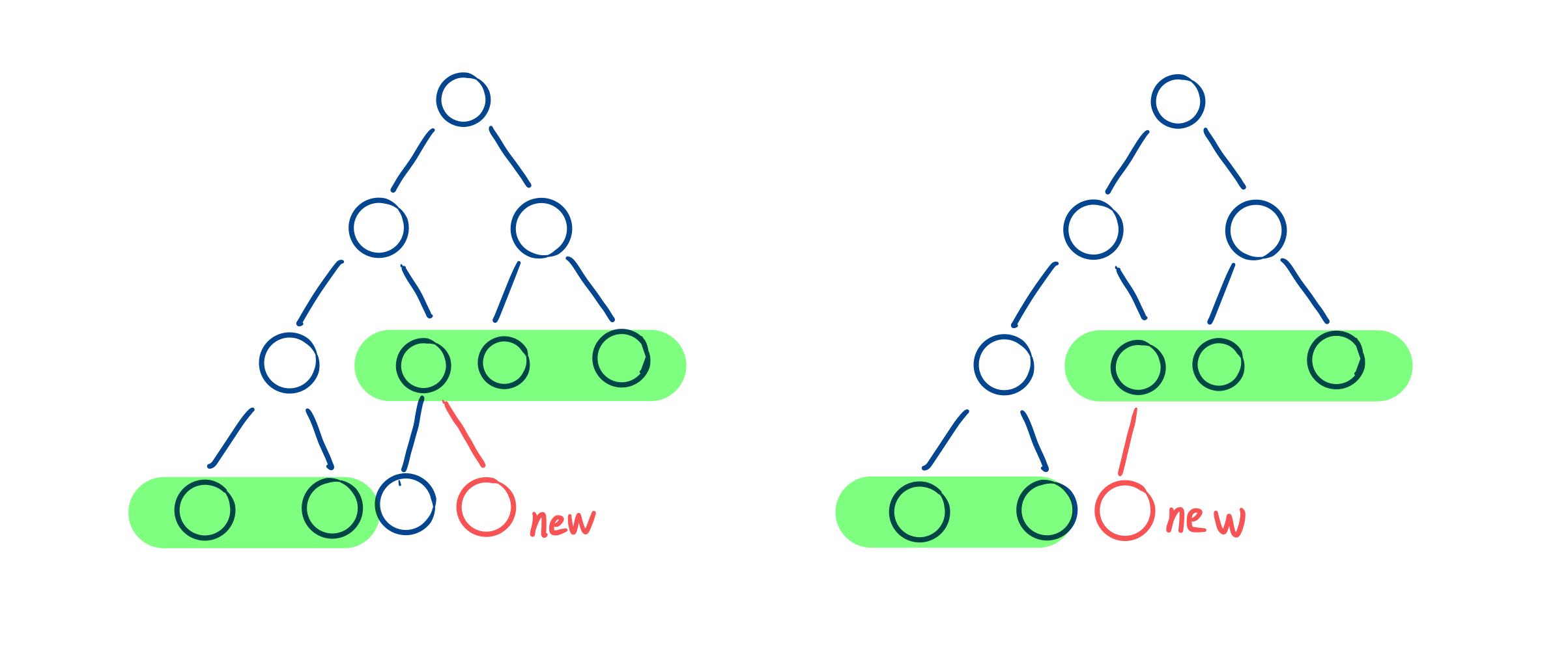
# 使用队列完成二叉树的层序遍历

通过观察可以发现新节点需要插入层次遍历时第一个出现的 “不完整的节点” （即不同时具有左右孩子节点）。如图中所示，绿色代表当前队列中的节点（规定节点的左右孩子均存在时才将它们一起先后压入队列)，当遍历到 “不完整的节点” 就找到了新节点插入的节点位置，“不完整的节点” 位于队列的头部。在 CBTInserter 函数中实现该过程，找到插入的位置，以及得到当前的队列。

插入操作时，先后检查队列头部节点的左右孩子，若左孩子缺失则将新节点插入其左孩子，右孩子缺失则插入右孩子。当队列头部节点的左右孩子都存在，则将其左右孩子压入队列尾部，队列的头部节点出队列，因为此时它已不是 “不完整的节点” 。更新后的队列的头部节点将是下一个 “不完整的节点”。按照规则依次处理接下来的插入操作。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class CBTInserter {
private:
    queue<TreeNode*> que;
    TreeNode* root;
public:
    CBTInserter(TreeNode* root) {
        this->root = root;
        que.push(root);
        while (que.front()->left != nullptr && que.front()->right != nullptr) {
            que.push(que.front()->left);
            que.push(que.front()->right);
            que.pop();
        }
       
    }
    
    int insert(int v) {
        TreeNode* node = new TreeNode(v);
        TreeNode* fa = que.front();
        if (fa->left == nullptr) {
            fa->left = node;
        }
        else {
            fa->right = node;
            que.push(fa->left);
            que.push(fa->right);
            que.pop();
        }
        return fa->val;
    }
    
    TreeNode* get_root() {
        return this->root;
    }
};

/**
 * Your CBTInserter object will be instantiated and called as such:
 * CBTInserter* obj = new CBTInserter(root);
 * int param_1 = obj->insert(v);
 * TreeNode* param_2 = obj->get_root();
 */