数据结构基础代码总结（树和图）
 2022-02-17  611f469c2c8a42436ca095b28ab2aefd 99+   42 m   6.3 k0 visits

数据结构基础代码总结（树和图）

树和图部分

# 一、树和二叉树

# 树的遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include <stdio.h>
#include <stdlib.h>

typedef struct BiTNode {
	ElemType data;
	struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

//先序遍历
//递归
void PreOrder(BiTree T) {
	if (T != NULL) {
		visit(T);
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}

//非递归
void PreOrder2(BiTree T) {
	InitStack(S);
	BiTree p = T;
	while (p || !IsEmpty(S)) {
		if (p) {
			visit(p);
			Push(S, p);
			p = p->lchild;
		} else {
			Pop(S, p);
			p = p->rchild;
		}
	}
}

//中序遍历
//递归
void InOrder(BiTree T) {
	if (T != NULL) {
		InOrder(T->lchild);
		visite(T);
		InOrder(T->rchild);
	}
}

//非递归
void InOrder2(BiTree T) {
	InitStack(S);
	BiTree p = T;
	while (p || !IsImpty(S)) {
		if (p) {
			push(S, p);
			p = p->lchild;
		} else {
			Pop(S, p);
			visit(p);
			p = p->rchild;
		}
	}
}

//后序遍历

void PostOrder(BiTree T) {
	if (T != NULL) {
		PostOrder(T->lchild);
		PostOrder(T->rchild);
		visit(T);
	}
}

//层次遍历
void LevelOrder(BiTree T) {
	InitQueue(Q);
	BiTree p;
	EnQueue(Q, T);
	while (!Empty(Q)) {
		DeQueue(Q, p);
		visit(p);
		if (p->lchild != NULL)
			EnQueue(Q, p->lchild);
		if (p->rchild != NULL)
			EnQueue(Q, p->rchild);
	}
}

# 线索二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <stdio.h>

typedef struct ThreadNode {
	ElemType data;
	struct ThreadNode *lchild, *rchild;
	int ltag, rtag;
} ThreadNode, *ThreadTree;

//中序线索二叉树
//递归
void InThread(ThreadTree &p, ThreadTree &pre) {
	if (p != NULL) {
		InThread(p->lchild, pre);	//递归，线索化左子树
		if (p->lchild == NULL) {	//左子树为空，建立前驱线索
			p->lchild = pre;
			p->ltag = 1;
		}
		if (pre != NULL && pre->rchild == NULL) {
			pre->rchild = p; //建立前驱节点的后继线索
			pre->rtag = 1;
		}
		pre = p;	//标记当前结点为刚刚访问过的结点
		InThread(p->rchild, pre);
	}
}

void CreatInThread(ThreadTree T) {
	ThreadTree pre = NULL;
	if (T != NULL) {
		InThead(T, pre);
		pre->rchild = NULL; //处理遍历的最后一个结点
		pre->rtag = 1;
	}
}

# 遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//中序线索树的遍历
ThreadNode *Firstnode(ThreadNode *p){
	while(p->ltag==0)
		p=p->lchild;
		return p;
}
ThreadNode *Nextnode(ThreadNode *p){
	if(p->rtag==0)
	return Firstnode(p->rchild);
	else
		return p->rchild;
}
//不含头结点的中序线索树的中序遍历
void Inorder(ThreadNode *T){
	for(ThreadNode *p=Firstnode(T);p!=NULL;p=Nextnode(p))
		visit(p);
}

# 二、图

# BFS

广度优先搜索
主要使用队列实现，对每个节点可能到达的路径进行入队出队判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <stdio.h>
#define MaxVertexNum 100
typedef char VertexType;
typedef int EdgeType;
int Max = 0x3f3f3f3f;

typedef struct {
	VertexType Vex[MaxVertexNum];
	EdgeType EdgeType[MaxVertexNum][MaxVertexNum];
	int vexnum, arcnum;
} Gragh;

//BFS遍历
bool visited[MaxVertexNum];
void BFSTraverse(Graph G) {
	for (int i = 0; i < G.vexnum; ++i)
		visited[i] = false;
	InitQueue(Q);
	for (int i = 0; i < G.vexnum; ++i)
		if (!visited[i])
			BFS(G, i);

}

void BFS(Graph G, int v) {
	visit(v);
	visited[v] = true;
	Enqueue(Q, v);
	while (!isEmpty(Q)) {
		DeQueue(Q, v);
		for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))
			if (!visited[w]) {
				visit(w);
				visited[w] = true;
				EnQueue(Q, w);
			}
	}
}

//BFS求单源最短路径
void BFS_MIN_Distance(Graph G, int u) {
	for (int i = 0; i < G.vexnum; i++)
		d[i] = Max; //初始化路径为无穷
	visited[u] = true;
	d[u] = 0;
	EnQueue(Q, u);
	while (!isEmpty(Q)) {
		DeQueue(Q, u);
		for (w = FirstNeighbor(G, u); w >= 0; w = NextNeighbor(G, u, w))
			if (!visited[w]) {
				visited[w] = true;
				d[w] = d[u] + 1;
				EnQueue(Q, w);
			}

	}
}

# DFS

深度优先搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool visited[MAX_VERTEX_NUM];
void DFSTraverse(Graph G){
	for(v=0;v<G.vexnum;++v)
		visited[v]=FALSE;
	for(v=0;v<G.vexnum;++v)
		if(!visited[v])
			DFS(G,v);
}
void DFS(Graph G,int v){
	visit(v);
	visited[v]=TRUE;
	for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
		if(!visited[w]){
			DFS(G,w);
	}
}

# 最小生成树

关于图的几个概念定义：

连通图：在无向图中，若任意两个顶点 vivi 与 vjvj 都有路径相通，则称该无向图为连通图。
强连通图：在有向图中，若任意两个顶点 vivi 与 vjvj 都有路径相通，则称该有向图为强连通图。
连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
生成树：一个连通图的生成树是指一个连通子图，它含有图中全部 n 个顶点，但只有足以构成一棵树的 n-1 条边。一颗有 n 个顶点的生成树有且仅有 n-1 条边，如果生成树中再添加一条边，则必定成环。
最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。
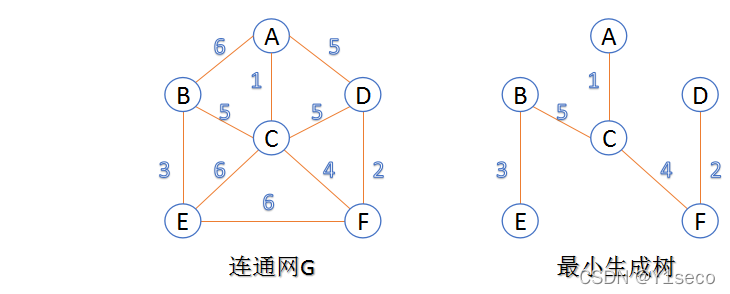
在这里插入图片描述

下面介绍两种求最小生成树算法

1.Kruskal 算法
此算法可以称为 “加边法”，初始最小生成树边数为 0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

把图中的所有边按代价从小到大排序；
把图中的 n 个顶点看成独立的 n 棵树组成的森林；
按权值从小到大选择边，所选的边连接的两个顶点 ui,viui,vi, 应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。
重复 (3), 直到所有顶点都在一颗树内或者有 n-1 条边为止。
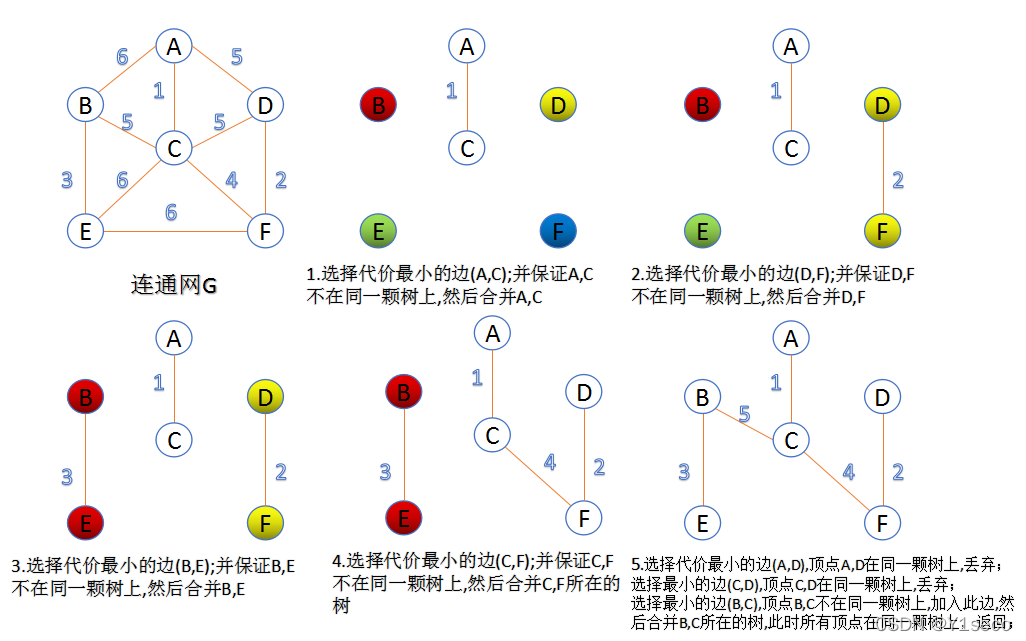
在这里插入图片描述

  1. Prim 算法
    此算法可以称为 “加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点 s 开始，逐渐长大覆盖整个连通网的所有顶点。

图的所有顶点集合为 VV；初始令集合 u={s},v=V−uu={s},v=V−u;
在两个集合 u,vu,v 能够组成的边中，选择一条代价最小的边 (u0,v0)(u0,v0)，加入到最小生成树中，并把 v0v0 并入到集合 u 中。
重复上述步骤，直到最小生成树有 n-1 条边或者 n 个顶点为止。
由于不断向集合 u 中加点，所以最小代价边必须同步更新；需要建立一个辅助数组 closedge, 用来维护集合 v 中每个顶点与集合 u 中最小代价边信息，：

1
2
3
4
5
6
struct
{
  char vertexData   //表示u中顶点信息
  UINT lowestcost   //最小代价
}closedge[vexCounts]

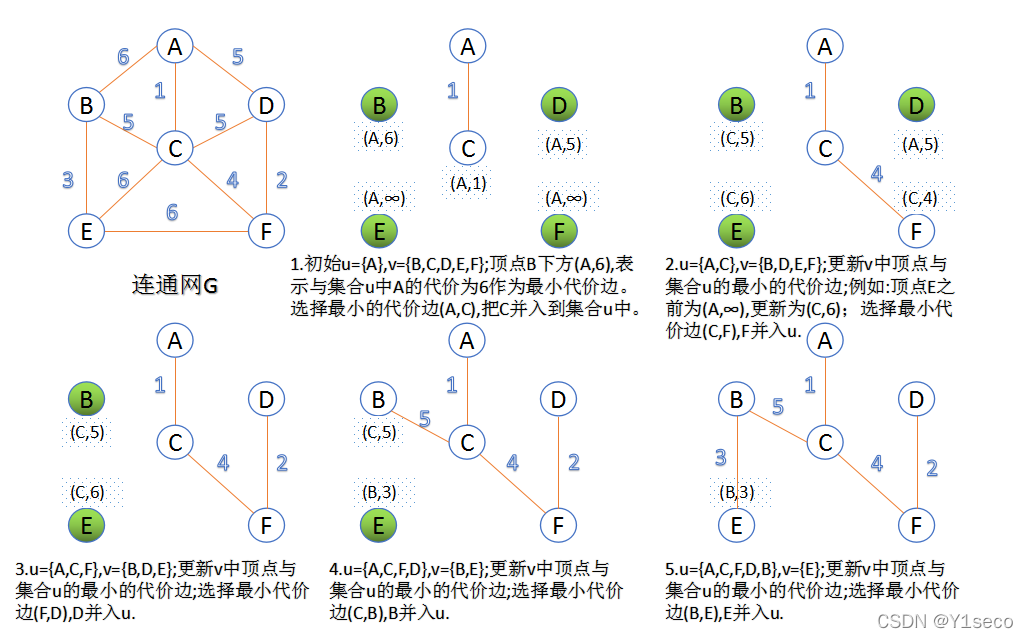
在这里插入图片描述

# Prim 算法

最小生成树是一个图的极小连通子图，它包含原图的所有顶点，并且所有边的权值之和尽可能小。

Prim 算法就是图的最小生成树算法之一，Prim 算法是一种求解加权无向连通图的 MST 问题的贪心算法。它能找出一个边的子集，使得其构成的树包含图中所有顶点，且边的权值之和最小。

Prim 算法以图的顶点为基础，从首个初始顶点，寻找到达其他顶点权值最小的边，并把该顶点加入到 “ 已到达顶点 ” 的集合中，此时，这个集合就是这个图的最小生成树。

一般用一维数组比较方便表达最小生成树，数组下标所对应的元素，代表该顶点在最小生成树当中的父亲节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
// 基于Prim算法实现最小生成树
#include <iostream>
#include <vector>
const int INF = 1e7;

using namespace std;

vector<vector<int>> Init() {
    int n, m;
    cout << "请输入带权无向图的定点数和边数(以空格隔开):" << endl;
    cin >> n >> m;
    vector<vector<int>> graph(n+1, vector<int>(n+1, INF));
    cout << "请依次输入" << m << "条边的开始节点，结束节点，权值(以空格隔开):" << endl;
    int start, end, wet;
    for (int i = 0; i < m; i++) {
        cin >> start >> end >> wet;
        graph[start][end] = wet;
        graph[end][start] = wet;
    }

    return graph;
}

int Prim(vector<vector<int>>& c, int u) {
    int n = c.size() - 1;
    // 定义数据结构lowcost[]，closest[]，s[]
    vector<int> lowcost(n+1);
    vector<int> closest(n+1);
    vector<bool> s(n+1);

    /// 1.初始化lowcost[]，closest[]，s[]
    s[u] = true;
    for (int i = 1; i <= n; i++) {
        if (i != u) {
            lowcost[i] = c[u][i];
            closest[i] = u;
            s[i] = false;
        }
        else
            lowcost[i] = 0;
    }


    // n个节点之间需要找最短路径n-1次
    for (int i = 0; i < n-1; i++) { 
        // 2.找最小
        int tmp = INF, t = u;
        for (int j = 1; j <= n; j++) {
            if (!s[j] && (lowcost[j] < tmp)) {   //!s[j]表示j节点V-U集合中
                t = j;
                tmp = lowcost[j];
            }
        }
        // 找不到，跳出循环
        if (t == u) break;

        // 将t加入集合U
        s[t] = true;  

        // 3.更新
        for (int j = 1; j <= n; j++) {
            if ((!s[j]) && (c[t][j] < lowcost[j])) {
                lowcost[j] = c[t][j];
                closest[j] = t;
            }
        }
    }

    // 4.打印最终结果
    int totalcost = 0;
    cout << "lowcost[]数组：";
    for (int i = 1; i <= n; i++) {
        cout << lowcost[i] << " ";
        totalcost += lowcost[i];
    }
    cout << endl;
    cout << "closest[]数组：";
    for (int i = 1; i <= n; i++) {
        cout << closest[i] << " ";
    }
    cout << endl;
    return totalcost;
}

// test main()
int main() {
    vector<vector<int>> graph = Init();
    int weight = Prim(graph, 1); // 1表示从1开始找
    cout << "\n最小生成树总的花费是：" << weight << endl;
}

实验结果
请输入带权无向图的定点数和边数 (以空格隔开):
7 12
请依次输入 12 条边的开始节点，结束节点，权值 (以空格隔开):
1 2 23
1 6 28
1 7 36
2 3 20
2 7 1
3 4 15
3 7 4
4 5 3
4 7 9
5 6 17
5 7 16
6 7 25
lowcost [] 数组：0 23 4 9 3 17 1
closest [] 数组：0 1 7 7 4 5 2

最小生成树总的花费是：57

D:\projects\test\x64\Release\test.exe (进程 1788) 已退出，返回代码为: 0。

# Kruskal 算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
/************************************************************************
CSDN 勿在浮沙筑高台 http://blog.csdn.net/luoshixian099算法导论--最小生成树（Prim、Kruskal）2016年7月14日
************************************************************************/
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define INFINITE 0xFFFFFFFF   
#define VertexData unsigned int  //顶点数据
#define UINT  unsigned int
#define vexCounts 6  //顶点数量
char vextex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };
struct node 
{
    VertexData data;
    unsigned int lowestcost;
}closedge[vexCounts]; //Prim算法中的辅助信息
typedef struct 
{
    VertexData u;
    VertexData v;
    unsigned int cost;  //边的代价
}Arc;  //原始图的边信息
void AdjMatrix(unsigned int adjMat[][vexCounts])  //邻接矩阵表示法
{
    for (int i = 0; i < vexCounts; i++)   //初始化邻接矩阵
        for (int j = 0; j < vexCounts; j++)
        {
            adjMat[i][j] = INFINITE;
        }
    adjMat[0][1] = 6; adjMat[0][2] = 1; adjMat[0][3] = 5;
    adjMat[1][0] = 6; adjMat[1][2] = 5; adjMat[1][4] = 3;
    adjMat[2][0] = 1; adjMat[2][1] = 5; adjMat[2][3] = 5; adjMat[2][4] = 6; adjMat[2][5] = 4;
    adjMat[3][0] = 5; adjMat[3][2] = 5; adjMat[3][5] = 2;
    adjMat[4][1] = 3; adjMat[4][2] = 6; adjMat[4][5] = 6;
    adjMat[5][2] = 4; adjMat[5][3] = 2; adjMat[5][4] = 6;
}
int Minmum(struct node * closedge)  //返回最小代价边
{
    unsigned int min = INFINITE;
    int index = -1;
    for (int i = 0; i < vexCounts;i++)
    {
        if (closedge[i].lowestcost < min && closedge[i].lowestcost !=0)
        {
            min = closedge[i].lowestcost;
            index = i;
        }
    }
    return index;
}
void MiniSpanTree_Prim(unsigned int adjMat[][vexCounts], VertexData s)
{
    for (int i = 0; i < vexCounts;i++)
    {
        closedge[i].lowestcost = INFINITE;
    }      
    closedge[s].data = s;      //从顶点s开始
    closedge[s].lowestcost = 0;
    for (int i = 0; i < vexCounts;i++)  //初始化辅助数组
    {
        if (i != s)
        {
            closedge[i].data = s;
            closedge[i].lowestcost = adjMat[s][i];
        }
    }
    for (int e = 1; e <= vexCounts -1; e++)  //n-1条边时退出
    {
        int k = Minmum(closedge);  //选择最小代价边
        cout << vextex[closedge[k].data] << "--" << vextex[k] << endl;//加入到最小生成树
        closedge[k].lowestcost = 0; //代价置为0
        for (int i = 0; i < vexCounts;i++)  //更新v中顶点最小代价边信息
        {
            if ( adjMat[k][i] < closedge[i].lowestcost)
            {
                closedge[i].data = k;
                closedge[i].lowestcost = adjMat[k][i];
            }
        }
    }
}
void ReadArc(unsigned int  adjMat[][vexCounts],vector<Arc> &vertexArc) //保存图的边代价信息
{
    Arc * temp = NULL;
    for (unsigned int i = 0; i < vexCounts;i++)
    {
        for (unsigned int j = 0; j < i; j++)
        {
            if (adjMat[i][j]!=INFINITE)
            {
                temp = new Arc;
                temp->u = i;
                temp->v = j;
                temp->cost = adjMat[i][j];
                vertexArc.push_back(*temp);
            }
        }
    }
}
bool compare(Arc  A, Arc  B)
{
    return A.cost < B.cost ? true : false;
}
bool FindTree(VertexData u, VertexData v,vector<vector<VertexData> > &Tree)
{
    unsigned int index_u = INFINITE;
    unsigned int index_v = INFINITE;
    for (unsigned int i = 0; i < Tree.size();i++)  //检查u,v分别属于哪颗树
    {
        if (find(Tree[i].begin(), Tree[i].end(), u) != Tree[i].end())
            index_u = i;
        if (find(Tree[i].begin(), Tree[i].end(), v) != Tree[i].end())
            index_v = i;
    }
 
    if (index_u != index_v)   //u,v不在一颗树上，合并两颗树
    {
        for (unsigned int i = 0; i < Tree[index_v].size();i++)
        {
            Tree[index_u].push_back(Tree[index_v][i]);
        }
        Tree[index_v].clear();
        return true;
    }
    return false;
}
void MiniSpanTree_Kruskal(unsigned int adjMat[][vexCounts])
{
    vector<Arc> vertexArc;
    ReadArc(adjMat, vertexArc);//读取边信息
    sort(vertexArc.begin(), vertexArc.end(), compare);//边按从小到大排序
    vector<vector<VertexData> > Tree(vexCounts); //6棵独立树
    for (unsigned int i = 0; i < vexCounts; i++)
    {
        Tree[i].push_back(i);  //初始化6棵独立树的信息
    }
    for (unsigned int i = 0; i < vertexArc.size(); i++)//依次从小到大取最小代价边
    {
        VertexData u = vertexArc[i].u;  
        VertexData v = vertexArc[i].v;
        if (FindTree(u, v, Tree))//检查此边的两个顶点是否在一颗树内
        {
            cout << vextex[u] << "---" << vextex[v] << endl;//把此边加入到最小生成树中
        }   
    }
}
 
int main()
{
    unsigned int  adjMat[vexCounts][vexCounts] = { 0 };
    AdjMatrix(adjMat);   //邻接矩阵
    cout << "Prim :" << endl;
    MiniSpanTree_Prim(adjMat,0); //Prim算法，从顶点0开始.
    cout << "-------------" << endl << "Kruskal:" << endl;
    MiniSpanTree_Kruskal(adjMat);//Kruskal算法
    return 0;
}

# Dijkstra 算法 (求单源最短路径问题)

# 算法原理

  • 适合求解有回路的带权图的最短路径
  • 可以求任意两个顶点的最短路径
  • 不适合求带负权值的最短路径问题

具体解释
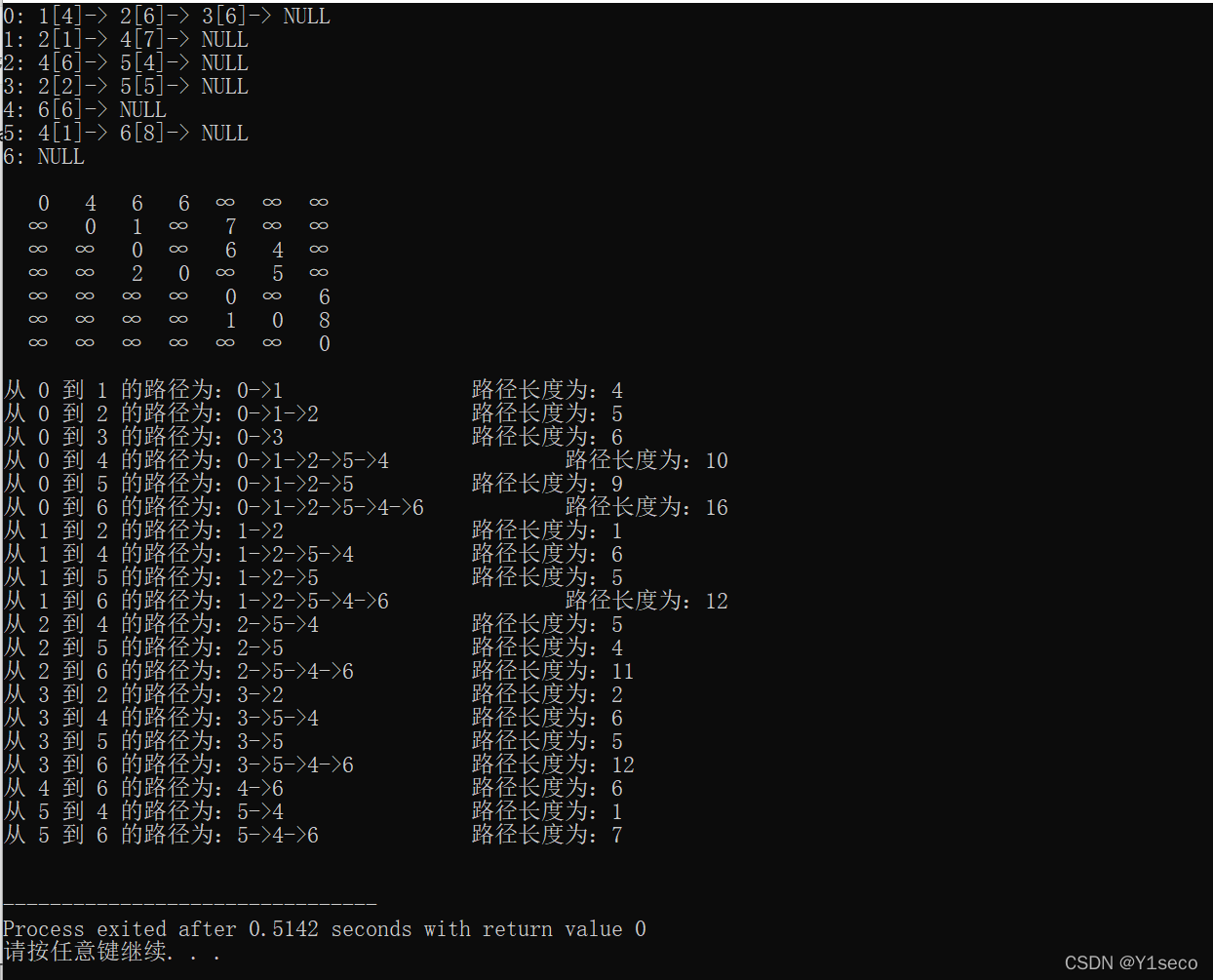
在这里插入图片描述

# 邻接矩阵实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
#include<iostream>
#include<iomanip>
#include<queue>
#include<vector>
using namespace std;

//用邻接矩阵构建有向图
#define MAX 999//表示无穷
#define MVNum 20//最大结点数
typedef int VertexType;//设置结点的数据类型为int型（方便后续修改成char...）
typedef int ArcType;//设置的权值为int型（方便后续修改成float...）

class Graph//Adjacency Matrix Graph有向图，用邻接矩阵表示
{
public:
	void Create();
	int LocateVex(VertexType u);//查找Graph中的顶点u，并返回其对应在顶点表中的下标，未找到则返回-1
	int firstadj(int v);
	int nextadj(int v, int w);
	void Dijkstra(VertexType start_point);//使用迪杰斯特拉算法打印单源最短路径
	void Show();//调试用，打印邻接矩阵
private:
	VertexType vexs[MVNum];//顶点表,将顶点保存的信息存入此处
	ArcType arcs[MVNum][MVNum];//邻接矩阵
	int vexnum, arcnum;//图当前的顶点数和边数
	vector<queue<VertexType>>path;//保存各结点最短路径的path[i]
	ArcType dist[MVNum];//最短路径大小
	bool solved[MVNum];//是否找到最短路径
};
int Graph::LocateVex(VertexType u)
{//查找Graph中的顶点u，并返回其对应在顶点表中的下标，未找到则返回-1
	int i;
	for (i = 0; i < this->vexnum; i++)
	{
		if (u == this->vexs[i])
			return i;
	}
	return -1;
}
int Graph::firstadj(int v)
{
	for (int i = 0; i < this->vexnum; i++)
	{
		if (this->arcs[v][i] != MAX)
			return i;
	}
	return -1;
}
int Graph::nextadj(int v, int w)
{
	for (int i = w + 1; i < this->vexnum; i++)
	{
		if (this->arcs[v][i] != MAX)
			return i;
	}
	return -1;
}
void Graph::Show()
{
	for (int i = 0; i < this->vexnum; i++)
	{
		for (int j = 0; j < this->vexnum; j++)
		{
			cout << setw(4) << this->arcs[i][j] << " ";
		}
		cout << endl;
	}
}
void Graph::Create()
{
	cout << "请输入总结点数和总边数:";
	cin >> this->vexnum >> this->arcnum;//输入总顶点数和总边数
	cout << "请输入各结点的信息:";
	for (int i = 0; i < this->vexnum; i++)
	{
		cin >> this->vexs[i];
	}
	//初始化邻接矩阵
	for (int i = 0; i < this->vexnum; i++)
	{
		for (int j = 0; j < this->vexnum; j++)
		{
			this->arcs[i][j] = MAX;
		}
	}
	//构造邻接矩阵
	for (int i = 0; i < this->arcnum; i++)
	{
		int v1, v2, w;
		cout << "请输入第" << i + 1 << "条边的起点和终点及其对应的权值:";
		cin >> v1 >> v2 >> w;
		int m = LocateVex(v1);
		int n = LocateVex(v2);
		this->arcs[m][n] = w;
	}
	return;
}
void Graph::Dijkstra(VertexType start_point)
{
	//初始化最短距离数组
	for (int i = 0; i < this->vexnum; i++)
	{
		this->dist[i] = MAX;
	}
	dist[this->LocateVex(start_point)] = 0;
	//初始化保存路径的向量
	queue<VertexType>temp;
	temp.push(start_point);
	for (int i = 0; i < this->vexnum; i++)
	{
		//（移到for外）queue<VertexType>temp;
		//temp.push(start_point);
		path.push_back(temp);
		//（不可行）path[i].push(start_point);//将起点作为最初始的路径加入每个结点对应的队列中
	}
	//初始化solved数组
	for (int i = 0; i < this->vexnum; i++)
	{
		solved[i] = false;
	}
	for (int i = 0; i < this->vexnum; i++)
	{
		if (this->arcs[this->LocateVex(start_point)][i] != MAX)
		{
			dist[i] = this->arcs[this->LocateVex(start_point)][i];
			path[i].push(this->vexs[i]);
		}
	}
	solved[this->LocateVex(start_point)] = true;
	for (int i = 0; i < this->vexnum; i++)
	{//返回地找
		ArcType mind = MAX;
		int v = i;
		for (int j = 0; j < this->vexnum; j++)
		{//一个劲地往前走
			//（移出for）int v = i;
			if (!solved[j] && dist[j] < mind)
			{
				mind = dist[j];
				v = j;
			}
			solved[v] = true;
			int w = this->firstadj(v);
			while (w != -1)
			{
				if (dist[v] + this->arcs[v][w] < dist[w])
				{
					dist[w] = dist[v] + this->arcs[v][w];
					path[w] = path[v];
					path[w].push(vexs[w]);
				}
				w = this->nextadj(v, w);
			}
		}
	}
	cout << "从结点" << start_point << "开始到各点的最短路径和路径长度如下:"<<endl;
	for (int i = 0; i < this->vexnum; i++)
	{
		if (dist[i] == MAX)
		{
			cout << "无法到达结点" << this->vexs[i] << endl;
		}
		else
		{
			cout << "抵达结点" << this->vexs[i] << "的最短路径:";
			int path_length = path[i].size();
			for (int j = 0; j < path_length; j++)
			{
				cout << path[i].front() << " ";
				path[i].pop();
			}
			cout << "长度为" << dist[i] << endl;
		}
	}
}
int main()
{
	Graph s;
	s.Create();
	s.Show();
	VertexType start_point;
	cout << "请输入起点:";
	cin >> start_point;
	s.Dijkstra(start_point);
	system("pause");
	return 0;
}


结果:
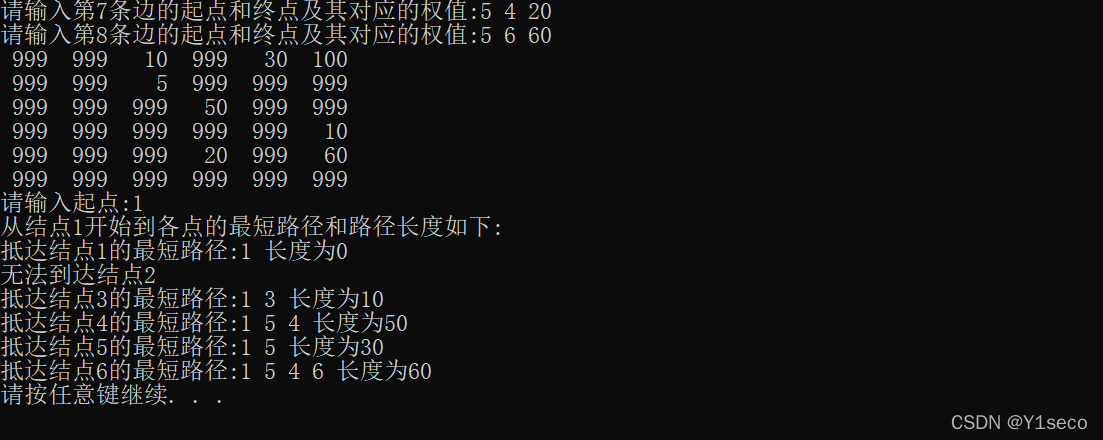
在这里插入图片描述
参考文章

# 邻接表实现

待定

# Floyd 算法 (求多源最短路径问题)

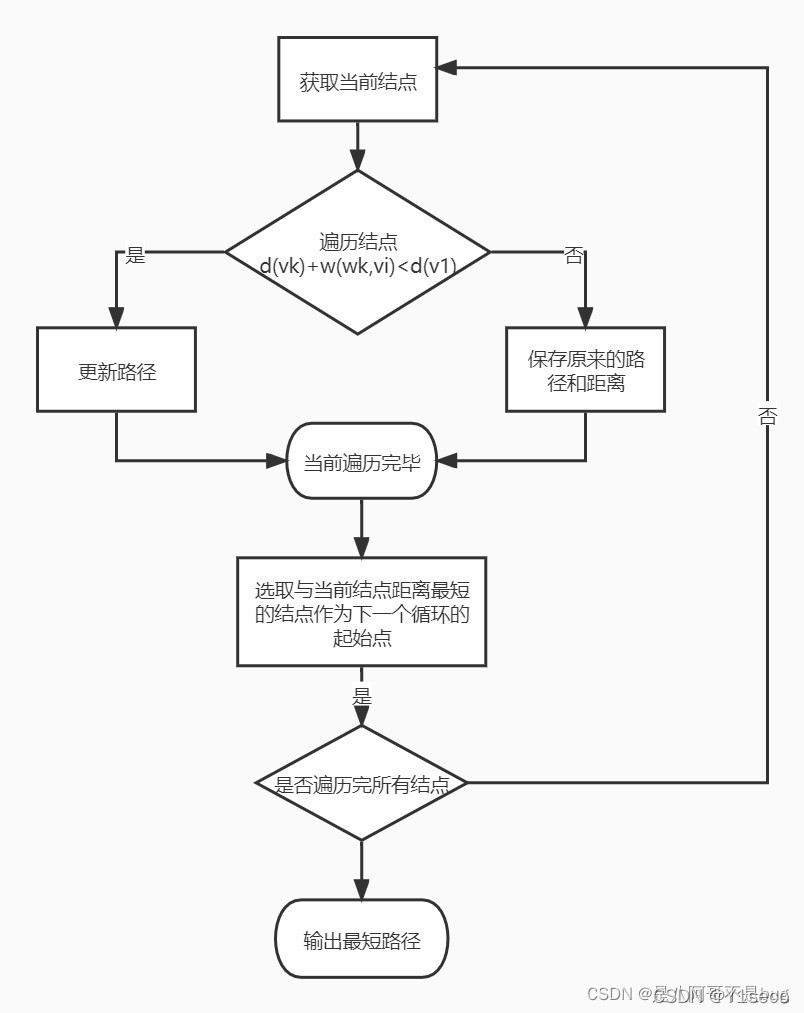
# 算法思想

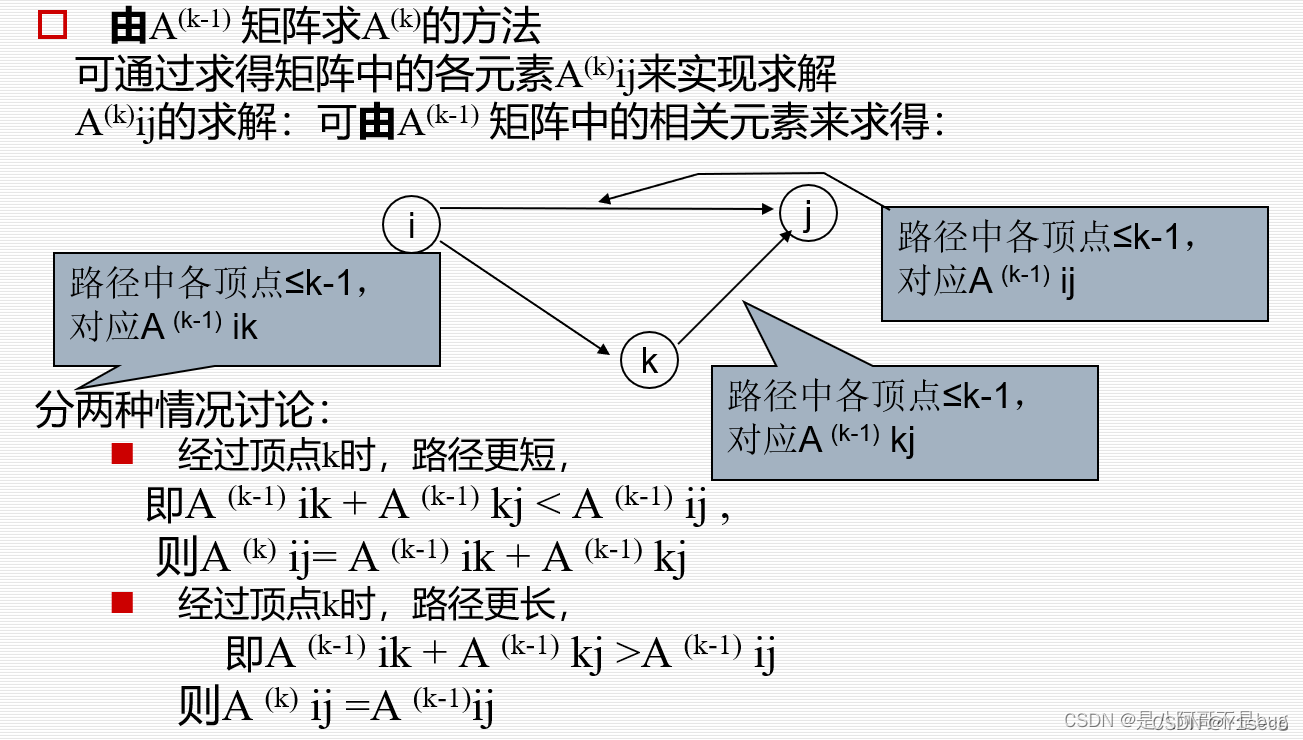
在这里插入图片描述
在这里插入图片描述
概括为迭代更新 i 经由 k 到 j 的最短路径.

# 算法原理

  1. 从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。
  2. 对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比已知的路径更短。如果是更新它。
  3. 把图用邻接矩阵 G 表示出来，如果从 Vi 到 Vj 有路可达，则 G [i][j]=d，d 表示该路的长度；否则 G [i][j]= 无穷大。定义一个矩阵 D 用来记录所插入点的信息，D [i][j] 表示从 Vi 到 Vj 需要经过的点，初始化 D [i][j]=j。把各个顶点插入图中，比较插点后的距离与原来的距离，G [i][j]= min ( G [i][j], G [i][k]+G [k][j] )，如果 G [i][j] 的值变小，则 D [i][j]=k。在 G 中包含有两点之间最短道路的信息，而在 D 中则包含了最短通路径的信息。
  4. 比如，要寻找从 V5 到 V1 的路径。根据 D，假如 D (5,1)=3 则说明从 V5 到 V1 经过 V3，路径为 {V5,V3,V1}，如果 D (5,3)=3，说明 V5 与 V3 直接相连，如果 D (3,1)=1，说明 V3 与 V1 直接相连。

# 邻接矩阵实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
#include<stdio.h>
#include<malloc.h>

#define MAXV 7					//最大顶点个数 
#define INF 32767				//定义 ∞
//∞ == 32767 ,int 型的最大范围（2位）= 2^(2*8-1)，TC告诉我们int占用2个字节，而VC和LGCC告诉我们int占用4个字节
//图：Graph
//顶点：Vertex
//邻接：Adjacency
//矩阵：Matrix
//表：List
//边：Edge 

typedef struct vertex {
	int number;					//顶点的编号 	
}VertexType; 					//别名，顶点的类型 

typedef struct matrix {
	int n;						//顶点个数
	int e;						//边数 
	int adjMat[MAXV][MAXV];		//邻接矩阵数组			
	VertexType ver[MAXV];		//存放顶点信息 
}MatGraph;						//别名，完整的图邻接矩阵类型

typedef struct eNode {
	int adjVer;					//该边的邻接点编号 
	int weiLGht;				//该边的的信息，如权值 
	struct eNode* nextEdLGe;	//指向下一条边的指针 
}EdgeNode; 						//别名，边结点的类型 

typedef struct vNode {
	EdgeNode* firstEdLGe;		//指向第一个边结点 
}VNode; 						//别名，邻接表的头结点类型 

typedef struct list {
	int n;						//顶点个数
	int e;						//边数
	VNode adjList[MAXV];		//邻接表的头结点数组 
}ListGraph;						//别名，完整的图邻接表类型 

//创建图的邻接表 
void createAdjListGraph(ListGraph*& LG, int A[MAXV][MAXV], int n, int e) {
	int i, j;
	EdgeNode* p;
	LG = (ListGraph*)malloc(sizeof(ListGraph));
	for (i = 0; i < n; i++) {
		LG->adjList[i].firstEdLGe = NULL;						//给邻接表中所有头结点指针域置初值 
	}
	for (i = 0; i < n; i++) {									//检查邻接矩阵中的每个元素 
		for (j = n - 1; j >= 0; j--) {
			if (A[i][j] != 0) {									//存在一条边 
				p = (EdgeNode*)malloc(sizeof(EdgeNode));		//申请一个结点内存
				p->adjVer = j;									//存放邻接点 
				p->weiLGht = A[i][j];							//存放权值
				p->nextEdLGe = NULL;

				p->nextEdLGe = LG->adjList[i].firstEdLGe;		//头插法 
				LG->adjList[i].firstEdLGe = p;
			}
		}
	}
	LG->n = n;
	LG->e = e;
}

//输出邻接表 
void displayAdjList(ListGraph* LG) {
	int i;
	EdgeNode* p;
	for (i = 0; i < MAXV; i++) {
		p = LG->adjList[i].firstEdLGe;
		printf("%d:", i);
		while (p != NULL) {
			if (p->weiLGht != 32767) {
				printf("%2d[%d]->", p->adjVer, p->weiLGht);
			}
			p = p->nextEdLGe;
		}
		printf(" NULL\n");
	}
}

//输出邻接矩阵
void displayAdjMat(MatGraph MG) {
	int i, j;
	for (i = 0; i < MAXV; i++) {
		for (j = 0; j < MAXV; j++) {
			if (MG.adjMat[i][j] == 0) {
				printf("%4s", "0");
			}
			else if (MG.adjMat[i][j] == 32767) {
				printf("%4s", "∞");
			}
			else {
				printf("%4d", MG.adjMat[i][j]);
			}
		}
		printf("\n");
	}
}

//邻接表转换为邻接矩阵
void ListToMat(ListGraph* LG, MatGraph& MG) {
	int i, j;
	EdgeNode* p;
	for (i = 0; i < MAXV; i++) {
		for (j = 0; j < MAXV; j++) {
			MG.adjMat[i][j] = 0;
		}
	}
	for (i = 0; i < LG->n; i++) {
		p = LG->adjList[i].firstEdLGe;
		while (p != NULL) {
			MG.adjMat[i][p->adjVer] = p->weiLGht;
			p = p->nextEdLGe;
		}
	}
	MG.n = LG->n;
	MG.e = LG->e;
}

//输出多源最短路径
void displayPath(MatGraph MG, int A[MAXV][MAXV], int path[MAXV][MAXV]) {
	int i, j, k;
	int s;
	int aPath[MAXV];										//存放一条最短路径（逆向）
	int d;													//顶点个数
	for (i = 0; i < MG.n; i++) {
		for (j = 0; j < MG.n; j++) {
			if (A[i][j] != INF && i != j) {					//若顶点 i 和 顶点 j 之间存在路径
				printf("从 %d 到 %d 的路径为：", i, j);
				k = path[i][j];
				d = 0;
				aPath[d] = j;								//路径上添加终点
				while (k != -1 && k != i) {					//路劲上添加中间点
					d++;
					aPath[d] = k;
					k = path[i][k];
				}
				d++;
				aPath[d] = i;								//路径上添加起点
				printf("%d", aPath[d]);						//输出起点
				for (s = d - 1; s >= 0; s--) {				//输出路径上其他顶点
					printf("->%d", aPath[s]);
				}
				printf("\t\t");
				printf("路径长度为：%d\n", A[i][j]);
			}
		}
	}
}

//Floyd算法
void Floyd(MatGraph MG) {
	int i, j, k;
	int A[MAXV][MAXV];
	int path[MAXV][MAXV];
	for (i = 0; i < MG.n; i++) {
		for (j = 0; j < MG.n; j++) {
			A[i][j] = MG.adjMat[i][j];
			if (i != j && MG.adjMat[i][j] < INF) {
				path[i][j] = i;							//顶点 i 到顶点 j 有边时
			}
			else {
				path[i][j] = -1;						//顶点 i 到顶点 j 无边时
			}
		}
	}
	for (k = 0; k < MG.n; k++) {						//一次考察所有顶点
		for (i = 0; i < MG.n; i++) {
			for (j = 0; j < MG.n; j++) {
				if (A[i][j] > A[i][k] + A[k][j]) {
					A[i][j] = A[i][k] + A[k][j];		//修改最短路径长度
					path[i][j] = path[k][j];			//修改最短路径
				}
			}
		}
	}
	displayPath(MG, A, path);							//输出最短路径
}

int main() {
	ListGraph* LG;
	MatGraph MG;

	int array[MAXV][MAXV] = {
		{  0,  4,  6,  6,INF,INF,INF},
		{INF,  0,  1,INF,  7,INF,INF},
		{INF,INF,  0,INF,  6,  4,INF},
		{INF,INF,  2,  0,INF,  5,INF},
		{INF,INF,INF,INF,  0,INF,  6},
		{INF,INF,INF,INF,  1,  0,  8},
		{INF,INF,INF,INF,INF,INF,  0}
	};

	int e = 12;
	createAdjListGraph(LG, array, MAXV, e);
	displayAdjList(LG);
	printf("\n");

	ListToMat(LG, MG);
	displayAdjMat(MG);
	printf("\n");

	Floyd(MG);
	printf("\n");

	return 0;
}

结果:
在这里插入图片描述
参考文章 1
参考文章 2

# 拓扑排序

# 原理

  1. 从 AOV 网中选择一个没有前驱的顶点并输出.
  2. 从网中删除该顶点和所有以它为起点的有向边.
  3. 重复直至 AOV 网为空或当前网中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环.

# 栈实现拓扑排序（邻接表实现）

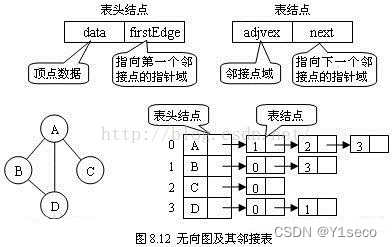
在这里插入图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include <iostream>
#include <fstream>
#include <stack>
#include <cstring>
using namespace std;

#define MAX_VERTEX_NUM 26

typedef struct ArcNode {
	int adjvex;
	struct ArcNode *nextarc;
	ArcNode() {
		nextarc = NULL;
	}
} ArcNode; //结点

typedef struct VNode {
	int data;
	ArcNode *firstarc;
	VNode() {
		firstarc = NULL;
	}
} VNode, AdjList[MAX_VERTEX_NUM];

typedef struct {
	AdjList vertices;
	int vexnum, arcnum;
} ALGraph;

bool TopologicalSort(ALGraph G, int *indegree) {
	stack<int> s;	//初始化栈

	int i, k;
	for (i = 1; i < G.vexnum + 1; i++) {
		if (!indegree[i])
			s.push(i); 	//入度为0的顶点入栈
	}

	int count = 0;	//记录当前已经输出的顶点数
	ArcNode *p;
	while (!s.empty()) {
		i = s.top();
		s.pop();
		cout << G.vertices[i].data << "->";
		count++;
		for (p = G.vertices[i].firstarc; p; p = p->nextarc) {
			k = p->adjvex;
			indegree[k]--; //将所有指向i的顶点的入度减一，并且将入度为0的顶点压入栈s
			if (!indegree[k])
				s.push(k);
		}
	}

	if (count < G.vexnum)
		return false;

	return true;
}

int main() {
	int i;
	ALGraph g;
	cout << "载入图中..." << endl;
	ifstream fin("in.txt");
	fin >> g.vexnum >> g.arcnum;
	for (i = 1; i < g.vexnum + 1; i++)
		g.vertices[i].data = i;

	int b, e;
	ArcNode *p;
	int *indegree = new int[g.vexnum + 1];
	//注意 int *a=new int(n);  申请一个整型变量空间，赋初值为n，并定义一个整型指针a指向该地址空间
	//int *indegree=(int *)malloc(sizeof(int)*(g.vexnum+1));
	memset(indegree, 0, sizeof(int) * (g.vexnum + 1));
	for (i = 1; i < g.arcnum + 1; i++) {
		fin >> b >> e;
		cout << "第" << i << "条边：" << b << "->" << e << endl;

		p = new ArcNode();
		p->adjvex = e;
		p->nextarc = g.vertices[b].firstarc;
		g.vertices[b].firstarc = p;
		indegree[e]++;
	}

	if (TopologicalSort(g, indegree))
		cout << "正常完成！" << endl;
	else
		cout << "该有向图有回路！" << endl;

	return 0;
}

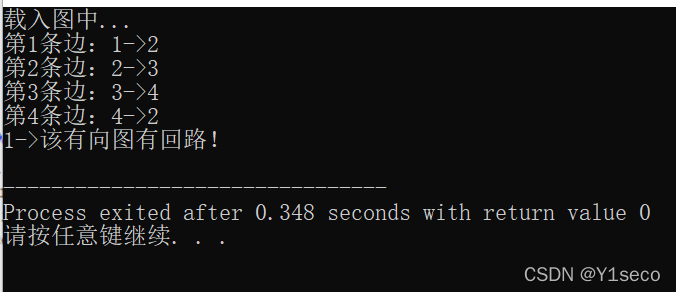
测试数据，新建 in.txt 文件输入内容

1）有环
4 4
1 2
2 3
3 4
4 2

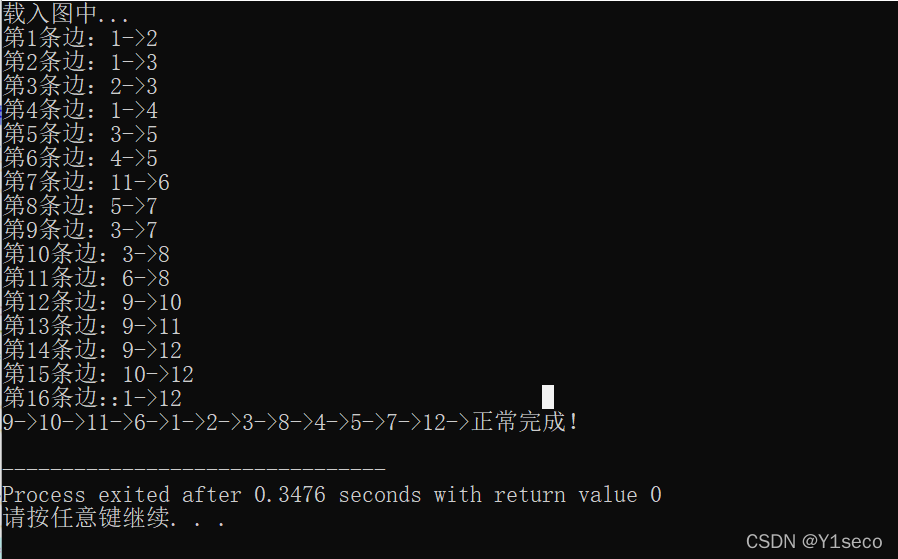
2）无环
12 16
1 2
1 3
2 3
1 4
3 5
4 5
11 6
5 7
3 7
3 8
6 8
9 10
9 11
9 12
10 12
1 12

结果:
在这里插入图片描述
在这里插入图片描述

参考文章
https://cloud.tencent.com/developer/article/1569368

数据结构基础代码总结（树和图）

https://y1seco.github.io/2022/02/17/【王道考研 数据结构 】基础算法代码复习总结 C语言(树和图）/

Author

y1seco

Posted on

2022-02-17

Updated on

2022-02-17

Licensed under

Like this article? Support the author with

Comments
Follow

:D 一言句子获取中...

Links

Recents

Categories

Archives

Tags

pwn5
leetcode2
随笔2
Kernel1
android1
arm1
flask1
go1
qemu1
vue1
数据结构1

Subscribe for updates

×